Neural Discrete Representation Learning (2017) 정리

Abstract

Vector Quantised Variational AutoEncoder (VQ-VAE)

• Differences with VAEs
  • The encoder network outputs discrete codes.
    • Discrete latent representation을 학습하기 위해 vector quantisation (VQ)를 도입 → VAE에서 자주 발생하는 'posterior collapse' 문제를 dhksghkgkf tn dlTdma.
  • The prior is learnt rather than static.
• Discrete latent representation + autoregressive prior → the model can generate high quality images, videos, and speech as well as doing high quality speaker conversion and unsupervised learning of phonemes.

---

1. Introduction

배경

• 이미지, 오디오, 비디오를 생성하는 분야에서 많은 발전이 있었고, few-shot learning, domain adaptation, reinforcement learning 등은 raw data로부터 representation을 학습하는 데에 크게 의존함.
• 그러나 unsupervised way로 일반적인 representation을 얻는 데에는 여전히 어려움이 존재함.
• Pixel domain에서 unsupervised model을 학습할 때에는 maximum likelihood와 reconstruction error가 가장 많이 사용됨.
  • 그러나 그 feature들이 사용되는 특정한 분야에 위 objectives의 유용성이 의존함.
• 본 논문에서는 maximum likelihood를 최적화하며 latent space에서 데이터의 중요한 feature를 보존할 수 있는 모델을 생성하고자 함.
  • 가장 좋은 generative model은 latent가 없지만 강력한 decoder를 가진 모델일 것 (e.g., PixelCNN)
  • 그러나 본 논문에서는 discrete and useful latent variables를 학습하는 것을 강조함.
    • Why discrete?
      • 언어는 본질적으로 이산적임 → speech를 sequence of symbols로 표현하는 것과 같음.
      • 이미지 역시 픽셀들로 이루어져 있기 때문에 이산적.

본 논문에서 제안하는 방법론

• A new generative models combining the variational autoencoder (VAE) framework with discrete latent representations through a novel parameterisation of the posterior distribution of (discrete) latents given an observation.
• 모델의 장점
  • simple to train
  • does not suffer from large variance
  • avoids the "posterior collapse" issue
    • Posterior collapse: approximate posterior가 prior를 그대로 mimic하여, 모델이 latent variable을 무시한 상태에서 학습이 진행되는 것.
      • e.g., x → z → x의 encoder-decoder 구조에서 latent variable z가 x에 관한 정보를 잘 담지 못하는 것
  • latent space를 효과적으로 사용하기 때문에 data space에서 여러 차원에 걸쳐 있는 중요한 특징들을 잘 모델링할 수 있음
    • e.g., objects span many pixels in images, phonemes in speech, the message in a text fragment, etc.
  • discrete random variable을 가지고 prior를 훈련시키기 때문에 interesting samples와 useful application을 얻을 수 있음
    • e.g., discover the latent structure of language without any supervision or prior knowledge about phonemes or words.

본 논문의 contributions

• Introducing the VQ-VAE model, which is simple, uses discrete latents, does not suffer from "posterior collapse" and has no variance issues.
• They showed that a discrete latent model (VQ-VAE) perform as well as its continuous model counterparts (VAE) in log-likelihood.
• When paired with a powerful prior, their samples are coherent and high quality on a wide variety of applications such as speech and video generation.
• They showed evidence of learning language through raw speech, without any supervision, and show applications of unsupervised speaker conversion.

---

2. Related work

A new way of training variational autoencoders with discrete latent variables

• NVIL estimator
  • uses a single-sample objective to optimize the variational lower bound
  • uses various variance-reduction techniques to speed up training
• VIMCO
  • optimizes a multi-sample objective → speeds up convergence 
• A new continuous reparametrization trick: Concrete or Gumbel-softmax distribution
  • a continuous distribution and has a temperature constant that can be annealed during training to converge to a discrete distribution in the limit
• However,
  • None of those methods close the performance gap of VAEs with continuous latent variables where one can use the Gaussian reparameterization trick which benefits from much lower variance in the gradients.
  • Most of these techniques are typically evaluated on relatively small datasets and the dimensionality of the latent distributions is small.

VAE의 decoder나 prior에서 autoregressive distribution이 사용되는 연구

• LSTM decoder / dilated convolutional decoders를 활용한 language modelling
• PixelCNNs

Neural networks를 사용한 image compression

• scalar quantisation to compress activateions for lossy image compression before arithmetic encoding
• compression model with vector quantization

---

3. VQ-VAE

input data x와 prior distribution $p(z)$가 주어졌을 때 VAE

• Encoder: discrete latent random variables z의 posterior distribution인 $q(z|x)$를 parameterize함.
• Decoder: $p(x|z)$를 예측함 → generative model

VAE의 posteriors와 priors는 일반적으로 Gaussian 분포를 따르다고 가정함.

반면 VQ-VAE는 posterior & prior distribution이 cagtegorical 하고, 이 분포로부터 생성된 samples는 embedding table을 indexing하고, 이 embedding을 decoder의 입력으로 사용함.

 

3.1. Discrete Latent variables

• a latent embedding space $e \in R ^ {K\times D}$
  • K: the size of the discrete latent space → K-way categorical
  • D: the dimensionality of each latent embedding vector $e_{i}$
• latent embedding space에 K개의 embedding vectors $e_{i} \in R^{D}$가 존재
• 모델이 입력 x를 받아 encoder에서 output $z_{e}(x)$를 생성
  • 이때 discrete latent variable z는 embedding space $e$에서 가장 가까운 vector를 찾음
  • $q(z=k|x) = \left\{\begin{matrix}
    1 for k=argmin_{j}||z_{e}(x) - e_{j}||_{2} \\ 0 otherwise
    \end{matrix}\right.   (1)$
  • prior $p(z)$를 uniform distribution으로 가정 → KL divergence term은 상수가 됨

• Encoder에서 생성된 representation $z_{e}(x)$는 embedding space에서 가장 가까운 벡터로 매핑된 후 decoder의 input으로 들어감.
  • $z_{q}(x) = e_{k}, where k = argmin_{j}||z_{e}(x) - e_{j}||_{2} $

 

3.2. Learning

학습 과정

• Forward computation: nearest embedding $z_{q}(x)$가 decoder에 전달됨.
• Backward pass: gradient $\bigtriangledown_{z}L $가 encoder에 그대로 전달됨.
  • Encoder를 학습시키기 위해 backpropagation을 사용하려고 하는데, 이때 미분가능한 term이 없음
    • Fig. 1의 붉은 선처럼 decoder input $z_{q}(x)$에서의 gradient를 encoder output $z_{e}(x)$에 그대로 복사해옴
    • ∵Encoder의 output representation과 decoder의 input이 동일한 D dimensional space를 공유하기 떄문에, reconstruction loss를 줄이기 위해 encoder가 본인의 출력을 어떻게 바꿔야 할지에 대한 정보를 gradient가 갖고 있음

Loss function $L = log p(x|z_{q}(x)) + ||sg[z_{e}(x)] - e||^{2}_{2} + \beta ||z_{e}(x) - sg[e]||^{2}_{2}$

• Reconstruction loss $log p(x|z_{q}(x))$: encoder & decoder를 최적화함
• $||sg[z_{e}(x)] - e||^{2}_{2}$
  • Embedding $e_{i}$는 reconstruction loss로부터 gradient를 받지 않기 때문에 vector quantization을 사용함
  • VQ objective가 $l_{2}$ error를 사용해서 embedding vector $e_{i}$를 encoder output $z_{e}(x)$ 쪽으로 이동시킴
• Commitment loss $\beta ||z_{e}(x) - sg[e]||^{2}_{2}$
  • embedding space는 dimensionless이기 때문에 $e_{i}$가 encoder parameter만큼 빠르게 학습되지 못할 수 있음
  • embedding과 encoder의 학습이 함께 이루어지게 하기 위해, encoder의 출력이 더이상 자라지 못하게 하기 위해 해당 항을 추가함
• sg: stop gradient operator
  • forward computation 시에는 identity로 정의되고 0의 partial derivative를 가짐
  • 연산자가 업데이트 되지 않도록 제한함
• Encoder: 1, 3번째 항을 최적화
• Decoder: 1번째 항을 최적화
• Embedding: 2번째 항에 의해 최적화됨

전체 모델 $log p(x)$ = $log p(x) = log \sum_{k}p(x|z_{k})p(z_{k})$

• decoder의 $p(x|z)$는 MAP (Maximum a posteriori) inference로 $z = z_{q}(x)$로 학습됨.
• 따라서 $z \neq z_{q}(x)$일 때는 $p(x|z)$를 구할 필요가 없으므로 $log p(x) \approx log p(x|z_{q}(x))p(z_{q}(x))$로 계산 가능
• Jensen's inequality에 의해 $log p(x) \geq  log p(x|z_{q}(x))p(z_{q}(x))$로도 계산 가능

 

3.3. Prior

$p(z)$: the prior distribution over the discrete latents → categorical distribution

• feature map 내에서 다른 z 값에 의존하여 autoregressive하게 만들어질 수 있음
• VQ-VAE 학습 시에 prior는 constant & uniform하게 유지됨
• 학습이 끝난 후 autoregressive 분포에 맞추어 ancestral sampling (미리 정의한 조건부확률로부터 샘플링)을 사용하여 x를 생성할 수 있음

---

4. Experiments

4.1. Comparison with continuous variables

model	VAE	VQ-VAE	VIMCO
lower bounds	4.51 bits/dim	4.67 bits/dim	5.14 bits/dim

 

4.2. Images

 

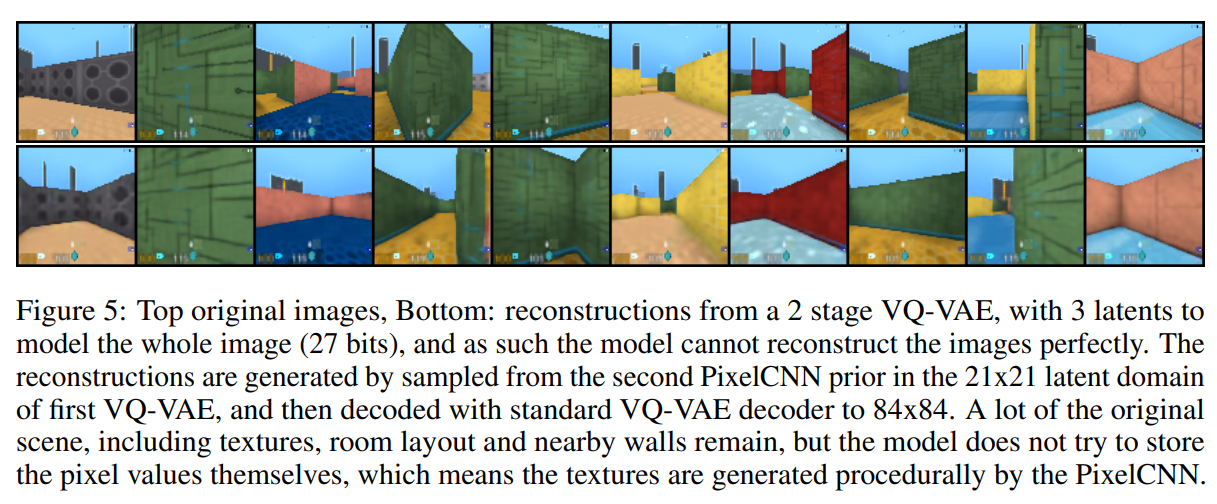
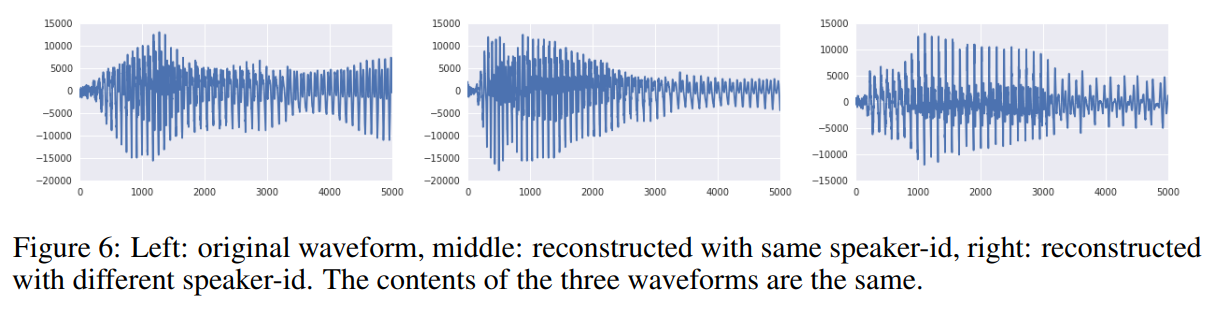
4.3. Audio

VQ-VAE can extract a latent space that only conserves long-term relevant information.

• reconstruction 결과 input으로 주어진 speech의 내용은 동일하게 유지했으나, 파형과 운율이 변화함.
  • VQ-VAE가 linguistic supervision 없이도 low-level feature에 무관한 high-level abstract space를 학습할 수 있고 speech의 내용만 인코딩할 수 있음을 보여줌

Unconditional samples 분석

• 오디오에서 추출한 compact & abstract latent representation이 주어졌을 때, 이걸로 prior를 학습시켜 모델이 데이터의 long-term dependency를 모델링하도록 함
• 40960 timesteps를 320 latent timesteps로 줄였음
• 원래 speech가 여러 소리가 섞여 있는 듯한 소리였다면 VQ-VAE로부터 생성된 샘플은 상대적으로 깨끗한 소리였음
• VQ-VAE가 raw audio waveform에서 unsupervised 방식으로 기본적인 phoneme-level language model을 모델링할 수 있음을 보여줌.

Speaker conversion

• speech의 content는 A speaker가 말한 내용이고, 목소리는 B speaker의 것인 sample을 생성할 수 있음

 

각 latents과 ground-truth phoneme-sequence 간의 비교

• 128개의 모든 가능한 latent values를 41개의 phoneme 중 하나에 대응시킴.
• 49.3%의 정확도를 얻음
• VQ-VAE가 unsupervised fashion으로 음소 정보를 학습할 수 있음.

 

4.4. Video

---

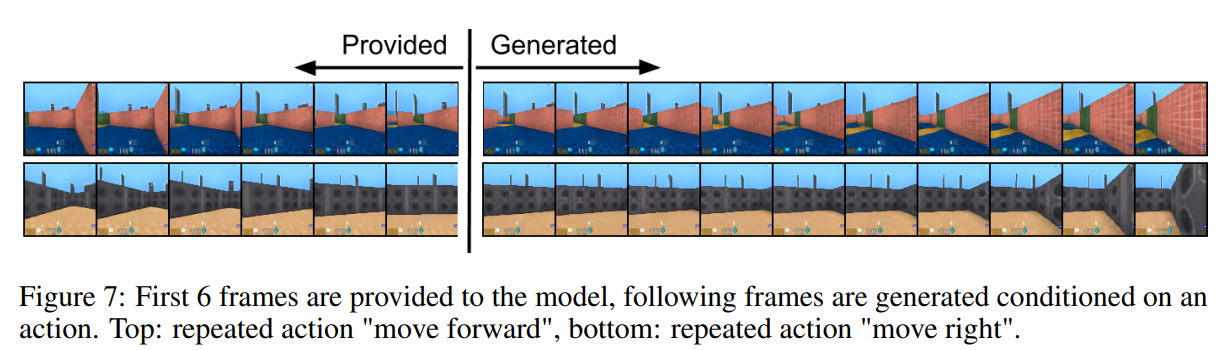
5. Conclusion

• VAE와 vector quantization을 결합하여 discrete latent representation을 얻을 수 있는 VQ-VAE라는 모델을 소개함.
• VQ-VAE는 long term dependency를 잘 모델링 할 수 있음.
• 원본 데이터를 작은 latent로 압축할 수 있고, 그렇게 압축된 latent는 discrete하고, continuous latent와 성능이 필적함.
• 데이터의 중요한 특징을 completely unsupervised manner로 포착 가능함.
• 이미지 뿐 아니라 오디오, 비디오 등의 분야에도 적용 가능함.

 

---

References

Van Den Oord, A., & Vinyals, O. (2017). Neural discrete representation learning. Advances in neural information processing systems, 30.

https://wain-together.tistory.com/8

2020/09/14

https://jaejunyoo.blogspot.com/2017/05/auto-encoding-variational-bayes-vae-3.html

초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (3)

http://datacrew.tech/vector-quantization/